PENGERTIAN GAYA, RESULTAN GAYA, MOMEN DAN TUMPUAN

Sebuah konstruksi dibuat dengan ukuran-ukuran fisik tertentu haruslah mampu menahan gaya-gaya yang bekerja dan konstruksi tersebut harus kokoh sehingga tidak hancur dan rusak. Konstruksi dikatakan kokoh apabila konstruksi tersebut dalam keadaan stabil , kestabilan tersebut akan terjadi bila gaya-gaya yang bekerja pada konstruksi dalam arah vertical dan horizontal saling menghilangkan atau sama dengan nol, demikian dengan momen-momen yg bekerja pada konstruksi tersebut pada setiap titik kumpul saling menghilangkan ata sama dengan nol.

Dalam analisa struktur terdapat metode penyelesaian dengan statis tertentu dan metode statis tak tentu. Pada metode statis tertentu berlaku prinsip berlaku prinsip gaya-gaya dalam arah vertical dan horizontal dan keseimbangan momen pada tumpuan dan dapat dinyatakan sebagai berikut :

∑Kv = 0
∑Kh =0
∑M = 0

Kv = Gaya Vertikal

Kh = Gaya Horizontal

M = Momen

GAYA

Gaya merupakan kekuatan yg dapat membuat benda dalam keadaan diam menjadi bergerak. Gaya biasa dilambangkan sebagai besaran yang mempunyai arah dan digambarkan dalam ilmu fisika seperti vector. Contohnya apabila pada sebuah benda dikerjakan pada sebuah gaya baik diangkat, ditarik atau didorong maka akan ada perlawanan terhadap gaya tersebut dan gaya perlawanan tersebut disebut dengan reaksi. Satuan untuk gaya ialah (Newton, Kg , Ton ).

RESULTAN GAYA

Apabila ada 2 buah gaya atau lebih bekerja pada sebuah benda maka dapat dilakukan penggabungan gaya-gaya tersebut yang disebut Resultan Gaya (R). Satuan untuk gaya ialah (Newton, Kg , Ton ).

F1 = Gaya 1

F2 = Gaya 2

FR = Resultan Gaya

MOMEN

Momen terjadi apabila sebuah gaya bekerja mempunyai jarak tertentu dari titik yang akan menahan momen tersebut dan besarnya momen tersebut adalah besarnya yang dikalikan dengan jaraknya. Satuan untuk momen ialah (N/m, Kg/m , Kg/cm, Ton/m, ).

TUMPUAN

Tumpuan ialah tempat perletakan konstruksi atau dukungan bagi konstruksi dalam meneruskan gaya-gaya yang bekerja ke pondasi.

Dalam ilmu analisa struktur dikenal 3 jenis tumpuan yaitu tumpuan sendi, tumpuan rol dan tumpuan jepit.

a. Tumpuan Sendi

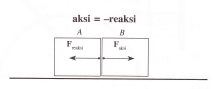
Tumpuan sendi sering disebut juga sebagai tumpuan engsel, karena cara kerjanya mirip dengan engsel. Tumpuan mampu memberikan reaksi gaya horizontal dan vertikal, artinya tumpuan sendi dapat menahan gaya vertikal maupun gaya horizontal dan tidak dapat menahan momen.

b. Tumpuan Rol

Tumpuan rol adalah tumpuan yang dapat bergeser kea rah horizontal sehingga tumpuan ini tidak dapat menahan gaya horizontal. Pada tumpuan rol terdapat roda yang dapat bergeser yang gunanya untuk mengakomodir pemuaian pada konstruksi sehingga konstruksi tidak rusak. Tumpuan rol hanya mampu memberikan reaksi arah vertikal saja, artinya tumpuan rol hanya bias menahan gaya secara vertikal saja dan tidak bias menahan gaya horizontal dan momen.

b. Tumpuan Jepit

Tumpuan jepit ialah merupakan tumpuan berupa balok yang terjepit pada tiang atau kolom. Pada tumpuan ini mampu memberikan reaksi terhadap gaya vertikal, horizontal bahkan mampu memberikan reaksi terhadap putaran momen.

Momen Gaya atau Torsi

Momen gaya atau torsi dapat didefinisikan dengan beberapa pengertian:

Torsi adalah gaya pada sumbu putar yang dapat menyebabkan benda bergerak melingkar atau berputar.
Torsi disebut juga momen gaya.
Momen gaya/torsi benilai positif untuk gaya yang menyebabkan benda bergerak melingkar atau berputar searah dengan putaran jam (clockwise), dan jika benda berotasi dengan arah berlawanan putaran jam (counterclockwise), maka torsi penyebabnya bernilai negatif.
Setiap gaya yang arahnya tidak berpusat pada sumbu putar benda atau titik massa benda dapat dikatakan memberikan Torsi pada benda tersebut.

Torsi atau momen gaya dirumuskan dengan:

$\tau = r \times F$

dimana:
$\tau$ adalah torsi atau momen gaya (Nm)
r adalah lengan gaya (m)
F adalah gaya yang diberikan tegak lurus dengan lengan gaya (N)

Jika gaya yang bekerja pada lengan gaya tidak tegak lurus, maka besar torsinya adalah:

$\tau = r \times F \times \sin \theta$

dimana $\theta$ adalah sudut antara gaya dengan lengan gaya.

Momen Inersia

Konsep momen inersia pertama kali diberikan oleh Leonhard Euler. Momen inersia didefinisikan sebagai kelembaman suatu benda untuk berputar pada porosnya, atau dapat dikatakan ukuran kesukaran untuk membuat benda berputar atau bergerak melingkar. Besar momen inersia bergantung pada bentuk benda dan posisi sumbu putar benda tersebut.

Momen inersia dirumuskan dengan:

$I = mr^2$

dimana:
I adalah momen inersia (kgm2)
r adalah jari-jari (m)
m adalah massa benda atau partikel (kg)

Benda yang terdiri atas susunan partikel atau benda-benda penyusunnya yang lebih kecil, jika melakukan gerak rotasi, maka momen inersianya sama dengan hasil jumlah semua momem inersia penyusunnya:

$I = \Sigma m_i \times r_i^2$

$I = (mr_1^2) + (mr_2^2) + (mr_3^2) + \cdots$

Momentum Sudut

Momentum sudut adalah ukuran kesukaran benda untuk mengubah arah gerak benda yang sedang berputar atau bergerak melingkar.

Momentum sudut dirumuskan dengan:

$L = I \omega$

$L = mvr$

dimana:
L adalah momentum sudut (kgm2s-1)
I adalah momen inersia benda (kgm2)
$\omega$ adalah kecepatan sudut benda (rad/s)
m adalah massa benda (kg)
v adalah kecepatan linear (m/s)
r adalah jarak benda ke sumbu putarnya (m)

Energi Kinetik Rotasi

Energi kinetik rotasi adalah energi kinetik yang dimiliki oleh benda yang bergerak rotasi yang dirumuskan dengan:

$Ek_r = \frac{1}{2} I \omega^2$

Jika benda tersebut bergerak secara rotasi dan juga tranlasi, maka energi kinetik totalnya adalah gabungan dari energi kinetik translasi rotasi dan energi kinetik rotasi:

$Ek_t = Ek + Ek_r$

$Ek_t = \frac{1}{2} mv^2 + \frac{1}{2} I \omega^2$

dimana:
Ekt adalah Energi kinetik total benda
Ek adalah energi kinetik translasi
Ekr adalah energi kinetik rotasi
m adalah massa benda (kg)
v adalah kecepatan linear (m/s)
I adalah momen inersia benda (kgm2)
$\omega$ adalah kecepatan sudut benda (rad/s)

Hukum Newton 2 Untuk Rotasi

Benda yang bergerak secara translasi menggunakan hukum newton II ( $\Sigma F = ma$ ) dan benda yang bergerak secara rotasi juga memakai konsep hukum Newton yang sama, akan tetapi besarannya memakai besaran-besaran rotasi. Sehingga, Hukum Newton II untuk benda yang bergerak secara rotasi atau bergerak melingkar memakai rumus:

$\tau = I \alpha$

dimana:
$\tau$ adalah total torsi yang bekerja pada benda
I adalah momen inersia benda
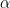$\alpha$ adalah percepatan sudut benda

Dibawah ini adalah tabel yang menganalogikan antara gerak translasi dan gerak rotasi

Besaran-besaran Pada Gerak Translasi			Besaran-besaran pada Gerak Rotasi
Besaran	Rumus	Satuan	Besaran	Rumus	Satuan
Jarak tempuh	s	m	Jarak tempuh sudut	q = s/r	rad
Kecepatan	V = s/t	m/s	Kecepatan sudut	$\omega = V/r$	rad/s
Percepatan	a = V/t	m/s2	Percepatan sudut	$\alpha = a/r$	rad/s2
Massa	m	kg	Momen inersia	I = mr2	kg . m2
Gaya	F = ma	N	Momen gaya/torsi	$\tau = rF$	Nm
Momentum	p = mv	kg . m/s	Momentum sudut	$L = I \omega$	kg . m2/s
Energi kinetik	$Ek = \frac{1}{2} mv^2$	Nm (Joule)	Energi kinetik rotasi	$Ek = \frac{1}{2} I \omega^2$	Nm (Joule)

Dibawah ini adalah tabel yang menyimpulkan hubungan antara gerak translasi dan gerak rotasi

Konsep	Gerak Translasi	Hubungan	Gerak Rotasi
Penyebab akselerasi	$\Sigma F$	$\tau = r \times F$	$\Sigma \tau$
Kesukaran untuk berakselerasi	m	$I = \Sigma m_i \times r_i^2$	I
Hukum newton 2	$\Sigma F = ma$		$\Sigma \tau = I \alpha$

Contoh Soal Dinamika Rotasi/Momen Gaya

Pada gambar diatas, sebuah katrol silinder pejal (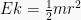 $Ek = \frac{1}{2}m r^2$ ) dengan massa 3kg dan berjari-jari 20 cm dihubungkan dengan dua buah tali yang masing-masing memiliki terpaut pada benda bermassa dimana m1 = 6kg dan m2 = 3kg. Sistem diatas berada dalam kondisi tertahan diam dan kemudian dilepaskan. Jika tidak terjadi gesekan pada lantai dengan, berapakah percepatan kedua benda tersebut?

Pembahasan:

Katrol:

$\Sigma \tau = I \alpha$

$(T_2 - T_1)r = \frac{1}{2}mr^2 \frac{a}{r}$

$T_2 - T_1 = \frac{1}{2}ma$

$T_2 - T_1 = \frac{1}{2}(3)a$

$T_2 - T_1 = 1,5a$

Sistem m2:

$\Sigma F = ma$

$W_2 - T_2 = m_2 a$

$30 - T_2 = 3a$

$T_2 = 30 - 3a$

Sistem m1:

$\Sigma F = ma$

$T_1 = m_1 a$

$T_1 = 6a$

Dengan mensubstitusi ketiga persamaan diatas, kita dapat mengetahui besar:

$T_2 - T_1 = 1,5a$

30 – 3a – 6a = 1,5a

30 – 9a = 1,5a

30 = 10,5a

a = 2,86m/s2

Menganalisis Karya Seni Rupa Murni

"Menganalisis Karya Seni Rupa Murni", 1. Pertama, yaitu Borobudur Pagi Hari Judul : Borobudur Pagi Hari Tahun : 1983 Ukuran : 150 cm x 200 cm Media : Cat Minyak “Borobudur Pagi Hari” merupakan salah satu karya Affandi yang terinspirasi oleh megahnya candi Borobudur dan lingkungan sekitar pada masa itu, saat Affandi melintas dan memperhatikan Borobudur di pagi hari. Obyek matahari selalu menarik perhatian di beberapa karya beliau sebagai fokus pendukung utama. Warna – warna dingin dan suasana tenang mendominasi lukisan ini karena melukiskan suasana pagi hari yang cerah . Dan dilukisan ini Affandy lebih nenonjolkan obyek alam sebagai latar belakang. Perpaduan warna yang digunakan semakin menghidupkan lukisan tersebut karena warna yang digunakan padu antara warna satu dengan warna yang lain. Dan dilukisan tersebut gambar candi Borobudur terlihat sangat jelas tanpa kita harus menganalisis makna lukisan tersebut. Dan bentuk mataharinya tidak menyerupai matahari tet...

toko mini

Search This Blog