Integral Substitusi dan Integral Parsial
Integral Substitusi dan Integral Parsial merupakan materi lanjutan dari pengertian integral dan integral tak tentu, serta konsep dasar integral lainnya. Silakan klik hyperlink tersebut jika anda ingin mempelajarinya terlebih dahulu.
Integral Substitusi
Teknik Integral Substitusi Dalam Fungsi Aljabar
Pada teknik ini, bentuk fungsi f(x) dapat diubah menjadi bentuk 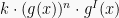 . Perhatikan bahwa jika U = g(x), maka
. Perhatikan bahwa jika U = g(x), maka  atau
atau 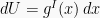 .
.
Jika
Maka, integral ini dapat diselesaikan dengan memisalkan U = g(x) dan  sehingga diperoleh persamaan:
sehingga diperoleh persamaan:
untuk  .
.
Jika saja  , maka:
, maka:
Sebagai contoh:
Jika 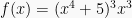 , untuk mendapat integralnya dengan memisalkan:
, untuk mendapat integralnya dengan memisalkan:
sehingga  .
.
Berdasarkan permisalan ini, maka persamaan integralnya menjadi:
Jika hasil integral diatas disubstitusi dengan permisalan U di peroleh:
Contoh diatas merupakan teknik substitusi pada integral tak tentu. Pada integral tertentu yang memiliki nilai pada interval 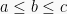 tertentu, maka interval tersebut harus disubstitusi ke dalam interval baru untuk variabel U. Sebagai contoh jika
tertentu, maka interval tersebut harus disubstitusi ke dalam interval baru untuk variabel U. Sebagai contoh jika 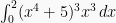 , untuk mendapat integralnya dengan memisalkan:
, untuk mendapat integralnya dengan memisalkan:
Sehingga  .
.
Untuk menciptakan persamaan integral dalam U, maka interval  dirubah menjadi :
dirubah menjadi :
Berdasarkan permisalan ini, maka persamaan integralnya menjadi:
Teknik Integral Substitusi Dalam Fungsi Trigonometri
Fungsi trigonometri sebagai integran, untuk beberapa kasus, tidak bisa langsung diintegralkan seperti rumus integral awal. Sehingga perlu juga dilakukan perubahan integran. Perubahan pada fungsi trigonometri dapat dilakukan sesuai dengan persamaan berikut:
Sama hal dengan fungsi aljabar, fungsi trigonometri dapat menggunakan teknik substitusi ini jika integran terdiri dari perkalian sebuah fungsi dengan fungsi turunannya sendiri. Pengoperasian juga sama dengan fungsi aljabar. Sebagai contoh, contoh jika 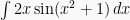 , untuk mendapat integralnya dengan memisalkan:
, untuk mendapat integralnya dengan memisalkan:
sehingga 2x dx = dU.
Berdasarkan permisalan ini, maka persamaan integralnya menjadi:
Jika hasil integral diatas disubstitusi dengan permisalan U, diperoleh:
Atau jika fungsi yang diturunkan adalah fungsi trigonometrinya langsung, maka sebagai contoh  , mendapat integralnya dengan memisalkan:
, mendapat integralnya dengan memisalkan:
sehingga sin x dx = – dU.
Berdasarkan permisalan ini, maka persamaan integralnya menjadi :
Jika hasil integral diatas disubstitusi dengan permisalan U, diperoleh :
Teknik Substitusi Dengan integran ![\sqrt[n]{ax+b} \sqrt[n]{ax+b}](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7Bax%2Bb%7D&bg=f9f9f9&fg=000000&s=0)
Pada teknik ini, dapat dimisalkan 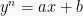 dan selanjutnya menyelesaikan integral dalam fungsi f(y) menggunakan teknik substitusi seperti di awal. Contoh
dan selanjutnya menyelesaikan integral dalam fungsi f(y) menggunakan teknik substitusi seperti di awal. Contoh 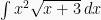 , dimisalkan :
, dimisalkan :
sehingga  atau 2y dx = dy.
atau 2y dx = dy.
Berdasarkan permisalan ini, maka persamaan integralnya menjadi:
Jika hasil integral diatas disubstitusi dengan permisalan y, diperoleh:
Teknik Substitusi Dengan integran  ,
,  , atau
, atau 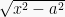
Integral dengan integran dalam bentuk akar diatas dapat dikerjakan dengan memisalkan dari bentuk diatas sebagai berikut:

Integral Parsial
Dalam pengintegralan, selain operasi biasa atau dengan teknik substitusi, ada teknik lain yaitu integral parsial. Teknik ini digunakan jika pada teknik sebelumnya tidak bisa digunakan. Teknik ini merupakan integral dari turunan hasil kali dua fungsi. Berikut ini adalah konsep integral parsial:
Jika y = U(x) . V(x), maka:
Jika y diganti UV maka:
Karena diketahui bahwa  dan
dan  , maka persamaan menjadi:
, maka persamaan menjadi:
d(UV) = V . dU + U . dV
U . dV = d(UV) – V . dU
Dengan mengintegralkan kedua ruas dalam persamaan diatas, diperoleh:
Rumus ntegral parsial:
Perlu diperhatikan untuk memilih U dan dV yang tepat agar pengintegralan memberikan hasil. (dV) harus dipilih yang dapat diintegralkan dengan rumus, sedangkan yang lain menjadi U.
Dalam integral parsial, terkadang bisa menurunkan U dan mengintegralkan dV secara berulang. Jika terjadi proses yang berulang, maka proses dapat diringkas. Sebagai contoh  adalah:
adalah:

Maka diperoleh hasil:
Contoh Soal Integral Substitusi dan Parsial dan Pembahasan
Contoh Soal 1
Tentukanlah hasil dari  .
.
Pembahasan 1:
Misalkan  dan
dan 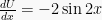 , maka
, maka
dU = -2 sin 2x dx
Sehingga,
Kemudian 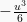 disubstitusi dengan nilai U menjadi :
disubstitusi dengan nilai U menjadi :
Contoh Soal 2
Tentukan hasil dari 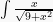
Pembahasan 2:
Misalkan trigonometrinya adalah:

Nilai  dan
dan  dan
dan  .
.
Sehingga:
Dengan segitiga diatas, nilai sec dan tan bisa diketahui. Sehingga:
Comments
Post a Comment