Matriks – Penjumlahan, Perkalian, Determinan, Invers
Penjumlahan dan Pengurangan Matriks
(Catatan: Untuk materi dasar tentang matriks, silakan buka di materi Matriks Dasar – Pengertian, Jenis, Transpose, dsb.)
Dua matriks atau lebih, dapat dijumlakan hanya jika memiliki ordo yang sama. Penjumlahan dilakukan dengan menjumlahkan elemen-elemen yang berposisi sama. Contoh:
Jika 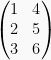 dan
dan 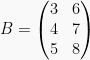 ,
,
maka:
Transformasi Geometri
Sama halnya dengan penjumlahan, pengurangan dapat dilakukan hanya jika dua matriks atau lebih, memiliki ordo yang sama. Pengurangan dilakukan terhadap elemen-elemen yang berposisi sama.
Contoh:
Jika 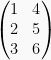 dan
dan 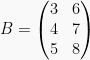 ,
,
maka:
Sifat dari penjumlahan dan pengurangan matriks:
- A + B = B + A
- (A + B) + C = A + (B + C)
- A – B ≠ B – A
Perkalian Matriks
Matriks dapat dikalikan dengan sebuah bilangan bulat atau dengan matriks lain. Kedua perkalian tersebut memiliki syarat-syarat masing-masing.
Perkalian Matriks dengan bilangan bulat
Suatu matriks dapat dikalikan dengan bilangan bulat, maka hasil perkalian tersebut berupa matriks dengan elemen-elemennya yang merupakan hasil kali antara bilangan dan elemen-elemen matriks tersebut. Jika matriks A dikali dengan bilangan r, maka 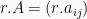 . Contoh:
. Contoh:
Jika 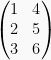 dan bilangan r = 2, maka:
dan bilangan r = 2, maka:
Perkalian matriks dengan bilangan bulat dikombinasikan dengan penjumlahan atau pengurangan matriks dapat dilakukan pada matriks dengan ordo sama. Berikut sifat-sifat perkaliannya:
- r(A + B) = rA + rB
- r(A – B) = rA – rB
Perkalian dua matriks
Perkalian antara dua matriks yaitu matriks A dan B, dapat dilakukan jika jumlah kolom A sama dengan jumlah baris B. Perkalian tersebut menghasilkan suatu matriks dengan jumlah baris sama dengan matriks A dan jumlah saman dengan matriks B, sehingga:

Elemen-elemen matriks  merupakan penjumlahan dari hasil kali elemen-elemen baris ke-i matriks A dengan kolom ke-j matiks B. Berikut skemanya:
merupakan penjumlahan dari hasil kali elemen-elemen baris ke-i matriks A dengan kolom ke-j matiks B. Berikut skemanya:

Misalkan matriks A memiliki ordo (3 x 4) dan matriks B memiliki ordo (4 x 2), maka matriks C memiliki ordo (3 x 2). Elemen C pada baris ke-2 dan kolom ke-2 atau a22 diperoleh dari jumlah hasil perkalian elemen-elemen baris ke-2 matriks A dan kolom ke 2 matriks B. Contoh:
maka:
Perlu diingat sifat dari perkalian dua matriks bahwa:
A x B ≠ B x A
Sebagai pembuktian, diketahui  dan
dan  maka:
maka:
Terbukti bahwa A x B ≠ B x A. Ada sifat-sifat lain dari perkalian matriks dengan bilangan atau dengan matriks lain, sebagai berikut:
- k(AB) = (kA)B
- ABC = (AB)C = A(BC)
- A(B + C) = AB + AC
- (A + B)C = AC + BC
Determinan Matriks
Determinan dari suatu matriks A diberi notasi tanda kurung, sehingga penulisannya adalah |A|. Determinan hanya bisa dilakukan pada matriks persegi.
Determinan matriks ordo 2×2
Jika 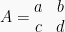 maka determinan A adalah:
maka determinan A adalah:
Determinan matriks ordo 3×3 (aturan Sarrus)
Jika 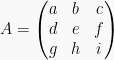 maka determinan A adalah:
maka determinan A adalah:

= aei + bfg + cdg – ceg – afh – bdi
Determinan matriks memiliki sifat-sifat berikut:
1. Determinan A = Determinan AT
2. Tanda determinan berubah jika 2 baris/2 kolom yang berdekatan dalam matriks ditukar

3. Jika suatu baris atau kolom sebuah determinan matriks memiliki faktor p, maka p dapat dikeluarkan menjadi pengali.
4. Jika dua baris atau dua kolom merupakan saling berkelipatan, maka nilai determinannya adalah 0.
5. Nilai determinan dari matriks segitiga atas atau bawah adalah hasil kali dari elemen-elemen diagonal saja.
Invers Matriks
Suatu matriks A memiliki invers (kebalikan) jika ada matriks B yang dapat membentuk persamaan AB = BA = I, dengan I adalah matriks identitas. Invers dari suatu matriks berordo (2 x 2) seperti 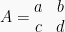 dapat dirumuskan sebagai:
dapat dirumuskan sebagai:
Invers matriks memiliki sifat-sifat berikut:
- AA-1 = A-1A = I
- (A-1)-1 = A
- (AB)-1 = B-1A-1
- Jika AX = B, maka X = A-1B
- Jika XA = B, maka X = BA-1
Contoh Soal Matriks dan Pembahasan
Contoh Soal 1
Suatu perkalian matriks 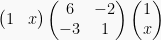 menghasilkan matriks nol. Tentukan nilai x yang memenuhui persamaan tersebut!
menghasilkan matriks nol. Tentukan nilai x yang memenuhui persamaan tersebut!
Pembahasan:
Maka nilai x yang memenuhi adalah x1 = 2 dan x2 = 3.
Contoh Soal 2
Jika matriks 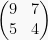 dan
dan 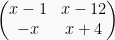 saling invers, tentukan nilai x!
saling invers, tentukan nilai x!
Pembahasan:
Diketahui bahwa kedua matriks tersebut saling invers, maka berlaku syarat AA-1 = A-1A = I.
Sehingga:
Sehingga pada elemen baris ke-1 kolom ke-1 memiliki persamaan:
9(x – 1) – 7x = 1
9x – 9 – 7x = 1
2x = 10
x = 5
Comments
Post a Comment