Persamaan Kuadrat

Persamaan kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Bentuk umumnya adalah:

$ax^2 + bx + c = 0$

Dengan a, b, merupakan koefisien, dan c adalah konstanta, serta $a \neq 0$ .

Penyelesaian atau pemecahan dari sebuah persamaan ini disebut sebagai akar-akar persamaan kuadrat. Akar-akar merupakan nilai dari variabel x yang memenuhi persamaan tersebut. Ketika nilai tersebut disubstitusikan ke dalam persamaan akan menghasilkan nilai nol.

Akar-akar Persamaan Kuadrat

Ada tiga metode dalam mencari akar-akar persamaan kuadrat 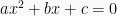$ax^2 + bx + c = 0$ yaitu:

Pemfaktoran

Metode ini mudah digunakan jika akar-akarnya merupakan bilangan rasional. Berikut ini tabel model persamaan kuadrat (PK) dan berbagai cara pemfaktorannya:

Saat menggunakan metode ini, pertama harus mengetahui terlebih dahulu model PK yang akan diselesaikan. Jika model PK sudah diketahui, maka pemfaktoran bisa dilakukan dalam bentuk sesuai dengan yang ada di kolom tabel di atas. Untuk mendapatkan nilai p, q, m dan n kalian harus memahami cara memfaktorkan suatu bilangan.

contoh :

Soal No. 1
Diberikan persamaan-persamaan kuadrat sebagai berikut:

a) p² − 16 = 0

b) x² − 3 = 0

c) y² − 5y = 0

d) 4 x² − 16 x = 0

Pembahasan
a) p² − 16 = 0
(p + 4)(p − 4) = 0
p + 4 = 0 → p = − 4
p − 4 = 0 → p = 4
Sehingga x = 4 atau x = − 4
Himpunan penyelesaian {−4, 4}

b) x² − 3 = 0
(x + √3)(x − √3) = 0
x = √3 atau x = − √3

c) y² − 5y = 0
y(y − 5) = 0
y = 0 atau y = 5

d) 4 x² − 16 x = 0
Sederhanakan dulu, masing-masing bagi 4 :
x² − 4 x = 0
x(x − 4) = 0
x = 0 atau x = 4

Soal No. 2
Diberikan persamaan-persamaan kuadrat sebagai berikut:
a) x² + 7x + 12 = 0
b) x² + 2x − 15 = 0
c) x² − 9 + 14 = 0
d) x² − 2x − 24 = 0
Faktorkan persamaan-persamaan kuadrat di atas!

Pembahasan
Bentuk umum persamaan kuadrat : ax² + bx + C = 0
Untuk nilai a = 1 seperti semua soal nomor 2, pemfaktoran sebagai berikut:
→ Cari dua angka yang jika di tambahkan (+) menghasilkan b dan jika dikalikan (x) menghasilkan c
a) x² + 7x + 12 = 0
+ → 7
x → 12
Angkanya : 3 dan 4
Sehingga
x² + 7x + 12 = 0
(x + 3)(x + 4) = 0
x = − 3 atau x = − 4

b) x² + 2x − 15 = 0
+ → 2
x → − 15
Angkanya : 5 dan − 3
Sehingga
x² + 2x − 15 = 0
(x + 5)(x − 3) = 0
x = − 5 atau x = 3

c) x² − 9 x + 14 = 0
+ → − 9
x → 14
Angkanya : −2 dan − 7
Sehingga
x² − 9x + 14 = 0
(x − 2)(x − 7) = 0
x = 2 atau x = 7

d) x² − 2x − 24 = 0
x² − 9 + 14 = 0
+ → − 2
x → − 24
Angkanya : − 6 dan 4
Sehingga
x² − 2x − 24 = 0
(x − 6)(x + 4) = 0
x = 6 atau x = − 4

Melengkapkan Kuadrat Sempurna

Metode melengkapkan kuadrat sempurna akan mudah digunakan jika koefisien a dibuat agar bernilai 1. PK dalam bentuk 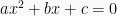$ax^2 + bx + c = 0$ diubah bentuk menjadi persamaan:

$(x + p)^2 = q$

Dengan p dan q adalah konstanta serta x adalah variabel. Nilai dari konstanta p dan q dari persamaan $x^2 + bx + c = 0$ didapatkan dengan cara:

$p = \frac{1}{2}b$

$q = (\frac{1}{2}b)^2 - c$

Perubahan tersebut dapat dibuktikan sebagai berikut :

$(x + p)^2 = q$

$(x + \frac{1}{2}b)^2 = (\frac{1}{2}b)^2 - c$

$x^2 + bx + (\frac{1}{2}b)^2 = (\frac{1}{2}b)^2 - c$

$x^2 + bx + c = 0$

contoh

Tentukan akar-akar persamaan kuadrat

x^2 + 8x + 12 = 0

dengan melengkapkan kuadrat sempurna.

Pada persamaan kuadrat tersebut, diketahui

a = 1

b = 8

, dan

c = 12

. Koefisien

x^2

sudah sama dengan

1

, jadi kita langsung ke langkah dua. Kurangi kedua ruas dengan nilai

c

\begin{aligned} x^2 + 8x + 12-12 &= 0-12 \\ x^2 + 8x &= -12 \end{aligned}

Tambahkan

\left( \frac{b}{2a} \right) ^{2} = \left( \frac{8}{2 \cdot 1} \right) ^{2} = 16

pada kedua ruas, sehingga

\begin{aligned} x^2 + 8x + 16 &= -12 + 16 \\ x^2 + 8x + 16 &= 4 \end{aligned}

Ubah ruas kiri menjadi bentuk kuadrat.

(x + 4)^2 = 4

Akarkan kedua ruas, sehingga diperoleh

\begin{aligned} x + 4 &= \pm 4 \\ x + 4 &= \pm 2 \\ x &= -4 \pm 2 \end{aligned}

Tentukan akar-akar persamaan kuadrat tersebut.

\begin{aligned} x_1 &= -4-2 = -6 \\ x_2 &= -4 + 2 = -2 \end{aligned}

Jadi, himpunan penyelesaiannya adalah

\{-6, -2\}

contoh

Tentukan akar-akar persamaan kuadrat

x^2 + 3x-10 = 0

dengan melengkapkan kuadrat sempurna.

Pada persamaan kuadrat tersebut, diketahui

a = 1

b = 3

, dan

c = -10

\begin{aligned} x^2 + 3x-10 &= 0 \\ x^2 + 3x &= 10 \end{aligned}

Tambahkan

\left( \frac{b}{2a} \right) ^{2} = \left( \frac{3}{2 \cdot 1} \right) ^{2} = \frac{9}{4}

pada kedua ruas, sehingga

\begin{aligned} x^2 + 3x + \frac{9}{4} &= 10 + \frac{9}{4} \\ \left( x + \frac{3}{2} \right)^2 &= \frac{49}{4} \\ x + \frac{3}{2} &= \pm \sqrt{ \frac{49}{4}} \\ x &= -\frac{3}{2} \pm \frac{7}{2} \end{aligned}

Tentukan akar-akar persamaan kuadrat tersebut.

\begin{aligned} x_1 &= -\frac{3}{2}-\frac{7}{2} = -\frac{10}{2} =-5 \\ x_2 &= -\frac{3}{2} + \frac{7}{2} = \frac{4}{2} = 2 \end{aligned}

Jadi, himpunan penyelesaiannya

\{-5, 2\}

Rumus abc

Metode rumus abc ini bisa digunakan jika pemfaktoran dan melengkapkan kuadrat sempurna tidak bisa dilakukan. Nilai dari akar-akar persamaan kuadrat 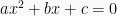$ax^2 + bx + c = 0$ didapatkan dari rumus abc berikut:

$x_{1,2} = \frac{- b \pm \sqrt{b^2 - 4ac}}{2a}$

Sehingga, akar-akarnya adalah

$x_1 = \frac{- b + \sqrt{b^2 - 4ac}}{2a}$

$x_2 = \frac{-b - \sqrt{b^2 - 4ac}}{2a}$

Jenis Akar-akar Persamaan Kuadrat

Jenis akar-akar persamaan kuadrat 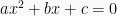$ax^2 + bx + c = 0$ dapat ditentukan dengan mengetahui nilai “Diskriminan” (D). Nilai diskriminan terdapat dalam rumus abc sebagai :

$D = b^2 - 4ac$

Sehingga rumus abc menjadi:

$x_{1,2} = \frac{-b \pm sqrt{D}}{2a}$

Tanda akar diskriminan 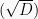$( \sqrt{D} )$ dalam rumus abc menentukan jenis dari akar-akar persaaman kuadrat, apakah bilangan real atau tidak real. Sehingga jenis akar-akar PK 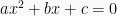$ax^2 + bx + c = 0$ adalah:

Jika D < 0 maka akar-akarnya tidak real.
Jika D > 0 maka akar-akarnya real ( $x_1, x_2 \in R$ ) dan berbeda ( $x_1 \neq x_2$ ).
Jika D = 0 maka akar-akarnya real ( $x_1, x_2 \in R$ ) dan sama atau kembar ( $x_1 = x_2$ ).

Jumlah dan Hasil Kali Akar-akar

Penjumlahan dan perkalian akar-akar persamaan $ax^2 + bx + c$ dapat dilakukan tanpa harus mengetahui nilai dari akar-akarnya. Jumlah akar-akar dapat diperoleh dengan :

$x_1 + x_2 = \frac{-b + \sqrt{b^2 - 4ac}}{2a} + \frac{-b - \sqrt{b^2 - 4ac}}{2a}$

$= \frac{-b + \sqrt{b^2 - 4ac} - b - \sqrt{b^2 - 4ac}}{2a}$

$= - \frac{2b}{2a} = - \frac{b}{a}$

Sedangkan hasil kali akar-akar dapat diperoleh dengan:

$x_1 \cdot x_2 = \frac{-b + \sqrt{b^2 - 4ac}}{2a} \cdot \frac{-b -\sqrt{b^2 - 4ac}}{2a}$

$= \frac{(-b)^2 - (b^2 - 4ac)}{(2a)^2}$

$\frac{4ac}{4a^2} = \frac{c}{a}$

Dari penjabaran tersebut dapat diketahui bahwa :

Penjumlahan akar-akar $x_1 + x_2 = -\frac{b}{a}$ .
Perkailan akar-akar $x_1 \cdot x_2 = \frac{c}{a}$ .

Ada beberapa bentuk pernyataan matematika yang bisa dirubah kedalam (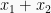 $x_1 + x_2$ ) dan ( 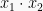$x_1 \cdot x_2$ ). Tujuan dari perubahan bentuk ini untuk memudahkan dalam peyelesaian persoalan. Perubahan ini dapat dilakukan dengan menggunakan sifat-sifat aljabar. Berikut ini sebagai contoh bentuk-bentuk perubahan:

$x_1 + x_2 = (x_1 + x_2)^2 - 2x_1 \cdot x_2$
$x_1^3 + x_2^3 = (x_1 + x_2)^3 - 3 (x_1 \cdot x_2)(x_1 + x_2)$
$\frac{1}{x_1} + \frac{1}{x_2} = \frac{(x_1 + x_2)}{(x_1 \cdot x_2)}$

contoh

Contoh Soal #1

Dengan menggunakan rumus ABC, tentukanlah akar-akar dari persamaan x² + 8x + 12 = 0

Jawab

Persamaan x² + 8x + 12 = 0 memiliki nilai a = 1, b = 8 dan c = 12.

x_1,2

=

–b ± √

b² – 4ac

2a

x_1,2

=

–8 ± √

8² – 4(1)(12)

2(1)

x_1,2

=

–8 ± √

64 – 48

2

x_1,2

=

–8 ± √

16

2

x_1,2

=

–8 ± 4

2

x_1,2 = –4 ± 2

x₁ = –4 – 2 = –6

x₂ = –4 + 2 = –2

Jadi akar-akarnya adalah x₁ = –6 atau x₂ = –2 dan bisa kita tuliskan HP = {–6, –2}.

Contoh Soal #2

Dengan menggunakan rumus kuadrat, tentukanlah akar-akar dari persamaan x² – 6x – 7 = 0

Jawab

Persamaan x² – 6x – 7 = 0 memiliki nilai a = 1, b = –6 dan c = –7.

x_1,2

=

–b ± √

b² – 4ac

2a

x_1,2

=

–(–6) ± √

(–6)² – 4(1)(–7)

2(1)

x_1,2

=

6 ± √

36 + 28

2

x_1,2

=

6 ± √

64

2

x_1,2

=

6 ± 8

2

x_1,2 = 3 ± 4

x₁ = 3 – 4 = –1

x₂ = 3 + 4 = 7

Jadi akar-akarnya adalah x₁ = –1 atau x₂ = 7 dan bisa kita tuliskan HP = {–1, 7}.

Menyusun Persamaan Kuadrat Baru

Suatu persamaan kuadrat baru dapat dibentuk jika diketahui nilai dari akar-akarnya. Hal tersebut dapat dilakukan dengan memasukan atau mensubstitusi nilai dari akar-akar yang telah diketahui kedalam persamaan

$(x - x_1)(x - x_2)$

atau

$x^2 - (x_1 + x_2)x + (x_1 . x_2)$

Suatu persamaan kuadrat baru juga dapat dibentuk walaupun tidak ada diketahui nilai dari akar-akarnya. Dengan syarat, akar-akar tersebut memiliki hubungan atau relasi dengan akar-akar dari PK yang lain.