Macam-macam Jenis Segitiga

Segitiga adalah bangun datar yang dibentuk oleh tiga garis lurus yang saling berpotongan. Segitiga dibentuk oleh 3 buah titik sudut yang letaknya tidak segaris dihubungkan. Untuk setiap segitiga selalu berlaku sifat-sifat yaitu; jumlah panjang dua sisi selalu lebih besar daripada panjang sisi segitiga; jumlah sudut-sudut sebuah segitiga adalah 180 derajat; sudut terbesar adalah sudut yang menghadap sisi terpanjang, sedangkan sudut terkecil adalah sudut yang menghadap sisi terpendek; besar sudut luar sama dengan jumlah dua sudut yang tidak berpenglurus dengan sudut luar tersebut. Tetang segitiga, banyak dibahas dalam ilmu Matematika.

Berdasarkan Panjang Sisi

Berdasarkan panjang sisinya, segitiga dibedakan menjadi berikut :

Segitiga sama kaki adalah jenis segitiga yang apabila ketiga sisinya sama panjang.

Segitiga sama sisi adalah jenis segitiga yang dua diantara sisi segitiga tersebut sama panjang.

Segitiga sembarang adalah jenis segitiga yang ketiga sisinya tidak sama.

Macam-macam Jenis Segitiga

Kita telah mengetahui bahwa dari tiga titik yang tidak terletak pada satu garis lurus, dapat dibuat satu bangun datar yang disebut segitiga.

Gambar di bawah ini menunjukkan tiga buah titik A, B, dan C yang tidak segaris. Jika ketiga titik tersebut dihubungkan, akan terbentuklah segitiga ABC. Biasanya segitiga dinotasikan dengan “D“, jadi segitiga ABC ditulis DABC.

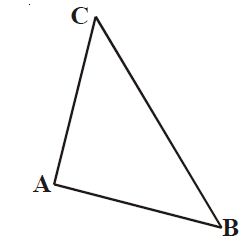Gambar: Segitiga ABC

Unsur-unsur yang terdapat dalam DABC adalah;

a. Titik A, B, dan C yang disebut titik sudut.

b. AB, BC, dan CA yang disebut sisi segitiga.

a. Jenis Segitiga Ditinjau dari Panjang Sisi-sisinya

Perhatikan gambar di bawah ini.

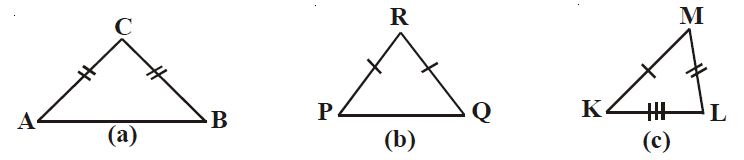Gambar: Segitiga a, b dan c

1. Gambar a, AC = BC , maka DABC disebut segitiga samakaki

2. Gambar b, PQ = QR = RP , maka DPQR disebut segitiga samasisi

3. Gambar c, ketiga sisinya mempunyai panjang yang berbeda-beda, maka DKLM disebut segitiga sembarang.

Berdasarkan uraian di atas:

Jenis segitiga ditinjau dari panjang sisinya ada 3 macam, yaitu segitiga sama kaki, segitiga sama sisi dan segitiga sebarang.

(i). Sifat-sifat Segitiga Sama kaki

Segitiga sama kaki mempunyai dua sisi yang sama panjang, maka segitiga itu juga mempunyai dua sudut sama besar, yaitu sudut saling berhadapan.

Sifat-sifat segitiga sama kaki adalah sebagai berikut;

a. Segitiga sama kaki, apabila diputar satu putaran penuh akan menempati bingkainya dengan tepat satu cara, maka segitiga samakaki mempunyai simetri putar tingkat satu.


b. Segitiga sama kaki mempunyai satu sumbu simetri. 

(ii). Sifat-sifat Segitiga Sama Sisi

Segitiga samasisi mempunyai tiga buah sisi yang sama panjang, maka ketiga sudutnya juga sama besar, yaitu 60o (Jumlah ketiga sudut D = 180o). Untuk mengetahui sifat-sifat segitiga samasisi lainnya, perhatikanlah uraian berikut ini.

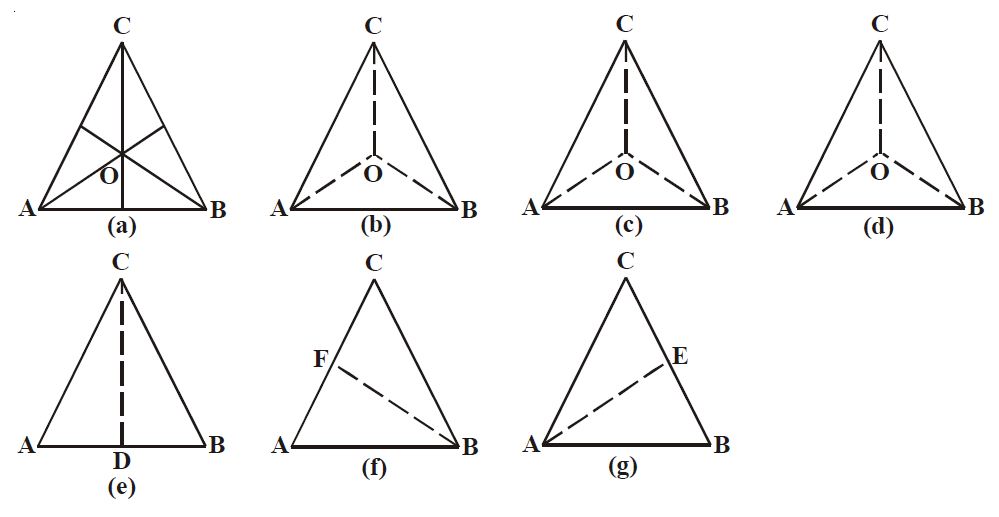Gambar: Segitiga ABC

Pada Gambar (b) – (d) terlihat bahwa segitiga ABC dapat menempati bingkainya tepat dengan 3 cara yaitu, diputar sejauh 120o dengan pusat titik O (lihat arah putaran) Gambar b, kemudian diputar sejauh 240o dengan pusat putaran O (Gambar c) dan diputar 360o (1 putaran penuh) dengan titik pusat O (Gambar d).

Jadi segitiga ABC mempunyai simetri putar tingkat 3. Sedangkan Gambar e, f, dan g dengan cara membalik dapat menempati bingkai secara tepat. Dalam hal ini segitiga ABC mempunyai 3 sumbu simetri. Pada gambar di atas, sumbu simetrinya adalah CD, BF, dan AE . Jadi, segitiga sama sisi dapat menempati bingkainya secara tepat dengan 6 cara.

Dari uraian di atas, sifat-sifat segitiga sama sisi adalah:

Segitiga sama sisi mempunyai simetri putar tingkat 3, tiga sumbu simetri, tiga sisi sama panjang, tiga sudut sama besar yaitu 60o, dan dapat menempati bingkainya dengan 6 cara.

b. Jenis segitiga ditinjau dari besar sudutnya

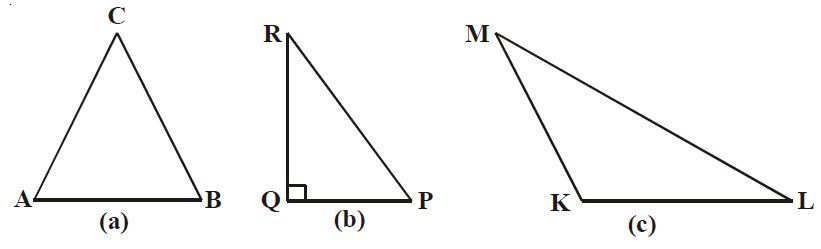Gambar: Macam macam Segitiga

Pada Gambar a besar ketiga sudutnya 􀂑Ð90o, jadi DABC disebut segitiga lancip. Pada Gambar b, besar salah satu sudutnya siku-siku yaitu 􀂑ÐPQR, sehingga segitiga PQR disebut segitiga siku-siku. Sedangkan, Gambar c, besar salah satu sudutnya tumpul, yaitu segitiga LKM, sehingga segitiga LKM disebut segitiga tumpul.

1. Segitiga dengan ketiga sudutnya lancip disebut segitiga lancip.
2. Segitiga dengan salah satu sudutnya 90o disebut segitiga siku-siku.
3. Segitiga dengan salah satu sudutnya tumpul disebut segitiga tumpul.

c. Jenis segitiga ditinjau dari panjang sisi-sisinya dan besar sudut-sudutnya

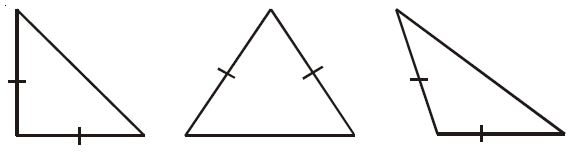Gambar: Macam-macam segitiga

Suatu segitiga dengan besar salah satu sudutnya 90o dan sisi-sisi siku-sikunya sama panjang disebut segitiga siku-siku sama kaki.

Suatu segitiga dengan sudut lancip dan dua sisinya sama panjang disebut segitiga lancip sama kaki.

Segitiga dengan salah satu sudutnya tumpul dan kedua sisinya sama panjang disebut segitiga tumpul sama kaki.

Demikian pembahasan tentang macam macam segitiga, jenis jenis segitiga, sifat sifat segitiga sama kaki, sifat sifat segitiga sama sisi, sifat sifat segitiga siku siku, sifat sifat segitiga sembarang.

Contoh Soal

1.Hitunglah keliling segitiga dengan panjang sisi-sisinya sebagai berikut.

a. 4,5 cm; 7,5 cm; dan 5,5 cm

b. 8 cm; 16 cm; dan 12 cm

c. 25 cm; 35 cm; dan 20 cm

Jawab =

Untuk mencari keliling segitiga kita dapat menjumlahkan ketiga sisi segitiga tersebut.

K = Sisi 1 + Sisi 2 + Sisi 3

a. 4,5 cm + 7,5 cm + 5,5 cm = 17,5 cm

b. 8 cm+ 16 cm + 12 cm = 36 cm

c. 25 cm + 35 cm + 20 cm = 80 cm

2. Hitunglah luas daerah masing-masing segitiga pada gambar di bawah ini.

Jawab =

(i) Luas segitiga ABC dapat dicari dengan persamaan:

L.ΔABC = ½ x alas x tinggi

L.ΔABC = ½ x AB x BC

L.ΔABC = ½ x 8 cm x 6 cm

L.ΔABC = 24 cm2

(ii) Luas segitiga DEF dapat dicari dengan persamaan:

L.ΔDEF = ½ x alas x tinggi

L.ΔDEF = ½ x 12 cm x 6 cm

L.ΔDEF = 36 cm2

(iii) Luas segitiga PQR dapat dicari dengan persamaan:

L.ΔPQR = ½ x alas x tinggi

L.ΔPQR = ½ x 16 cm x 4 cm

L.ΔPQR = 32 cm

(iv) Luas segitiga STU dapat dicari dengan persamaan:

L.ΔSTU = ½ x alas x tinggi

L.ΔSTU = ½ x ST x RU

L.ΔSTU = ½ x 5 cm x 4 cm

L.ΔSTU = 10 cm2