Skip to main content

Pengertian kerucut

Pengertian kerucut

Kerucut adalah bangun ruang sisi lengkung yang menyerupai limas segi-n beraturan yang bidang alasnya berbentuk lingkaran.
Menurut kamus besar bahasa Indonesia, kerucut berarti gulungan meruncing dari kertas atau daun atau kelopak bamu untuk tempat kacang dan sebagainya.
Atau pengertian lain menurut sumber yang sama, bahwa kerucut adalah benda atau ruang yang beralas bundar dan merunjung sampai ke satu titik.

Asal-usul kerucut

Kerucut dapat dibentuk dari sebuah segitiga siku-siku yang diputar sejauh 360 derajat, dimana sisi siku-sikunya sebagai pusat putaran.
Perhatikan gambar berikut ini!
Pengertian Kerucut, Unsur-unsur Kerucut dan Jaring-jaring Kerucut
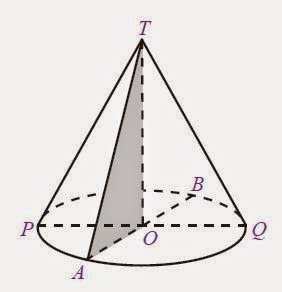Gambar: Asal Kerucut
Kerucut pada gambar tersebut di atas dibentuk dari segitiga siku-siku TOA yang diputar satu putaran penuh (360 derajat) dengan sisi TO sebagai pusat putaran.

Unsur-unsur kerucut

Perhatikan gambar kerucut berikut ini!
Pengertian Kerucut, Unsur-unsur Kerucut dan Jaring-jaring Kerucut
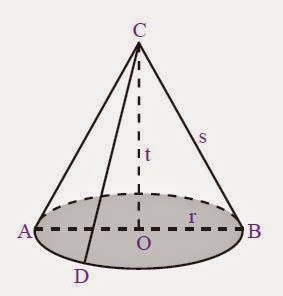
Berdasarkan gambar kerucut tersebut di atas, dapat disimpulkan bahwa kerucut tersebut memiliki unsur-unsur sebagai berikut;
a. Bidang alas, yaitu sisi yang berbentuk lingkaran (daerah yang diarsir).
b. Diameter bidang alas (d), yaitu ruas garis AB.
c. Jari-jari bidang alas (r), yaitu garis OA dan ruas garis OB.
d. Tinggi kerucut (t), yaitu jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
e. Selimut kerucut, yaitu sisi kerucut yang tidak diarsir.
f. Garis pelukis (s), yaitu garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.
Hubungan antara r, s, dan t pada kerucut tersebut di atas dapat dinyatakan dengan persamaan-persamaan berikut, yang bersumber dari teorema pythagoras, yaitu:
s2 = r2 + t2
r2 = s2 − t2
t2 = s2 − r2

Jaring-jaring kerucut

Tidak banya jenis dan model untuk jaring kerucut, karena kerucut merupakan bangun ruang sisi lengkung yang bentuknya sangat relatif.
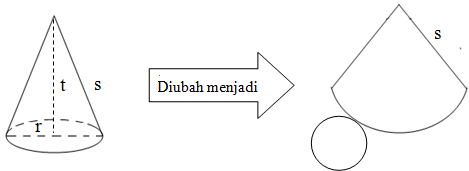
Berikut ini merupakan salah satu contoh jaring-jaring pada kerucut, sebenarnya masih dapat dikembangkan menjadi model-model yang lain.
Pengertian Kerucut, Unsur-unsur Kerucut dan Jaring-jaring Kerucut

Rumus Volume Kerucut

Perhatikan gambar di bawah ini! 
Limas (a) dan Kerucut (b)
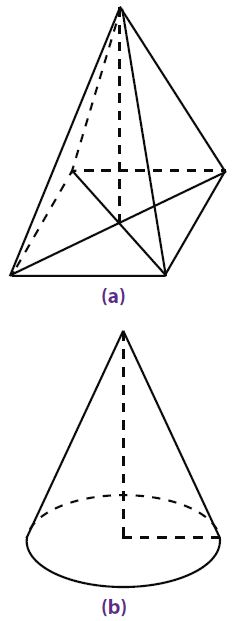Gambar: Limas (a) dan Kerucut (b)
Dapatkah kamu menemukan persamaan antara gambar (a) dan gambar (b)? Pada dasarnya, kerucut merupakan limas karena memiliki titik puncak sehingga volume kerucut sama dengan volume limas, yaitu ⅓ kali luas alas kali tinggi. Oleh karena alas kerucut berbentuk lingkaran, volume kerucut dinyatakan oleh rumus sebagai berikut.
Rumus Volume Kerucut dan Contoh Soal Volume kerucut

Contoh Soal Volume Kerucut

1. Hitunglah volume suatu kerucut yang memiliki jari-jari 2,5 dm dan tinggi 9 dm.

Jawab :

Diketahui:
r = 2,5 dm
t = 9 dm
Ditanyakan: volume kerucut?
Penyelesaian:
Volume kerucut = ⅓πr2t
                           = ⅓· 3,14 · (2,5)2 · 9
                           = 58,875 dm3
Jadi, volume kerucut tersebut adalah 58,875 dm3
2. Jika panjang OA = 30 mm dan TA = 5 cm, hitunglah volume kerucut di bawah ini.
Rumus Volume Kerucut dan Contoh Soal Volume kerucut

Jawab :

Diketahui :
OA = r = 30 mm = 3 cm
TA = s = 5 cm
Ditanyakan : volume kerucut
Jawab:
t2 = s2 − r2
    = 52 − 32
    = 25 − 9
    = 16
t   = √16
    = 4
Tinggi kerucut = 4 cm.
Volume kerucut = ⅓πr2t
                           = ⅓· 3,14 · (3)2 · 4
                           = 37,68
Jadi, volume kerucut tersebut adalah 37,68 cm3

Demikian pembahasan secara sederhana namun lengkap tentang pengertian kerucut, unsur-unsur kerucut dan jaring-jaring kerucut.

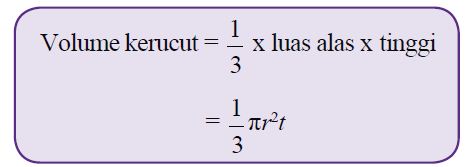
Comments

Post a Comment

Popular posts from this blog

pengertian Kepala Silinder (Cylinder Head)

Kepala Silinder (Cylinder Head)  adalah komponen utama mesin yang diikatkan pada bagian atas blog silinder dan merupakan tempat dari ruang bakar, busi dan mekanisme katup  (valve).  Kepala silinder juga merupakan dudukan dari saluran masuk dan saluran buang. Kepala silinder ada yang dibuat dari besi tuang yang tahan terhadap temperatur dan tekanan tinggi selama mesin bekerja. Namun kebanyakan mobil sekarang banyak yang dibuat dari paduan alumunium, dengan bahan ini kepala silinder lebih baik dalam hal pendinginan. Dari sisi beratnya juga lebih ringan. Kepala Silinder Kepala silinder juga dilengkapi dengan mantel pendingin yang dialiri oleh air pendingin, tujuannya tentu untuk mendinginkan kepala silinder, katup-katup dan busi. Fungsi Kepala Silinder Seperti yang telah disinggung di atas bahwa kepala silinder dalam mesin kendaraan memiliki beberapa fungsi, yaitu :  1. Sebagai tempat mekanisme katup   Jika kita bongkar kepala silinder m...
Post a Comment
Read more

Komponen Mekanisme Katup OHV dan OHC

Komponen Mekanisme Katup OHV dan OHC + Fungsinya  - Mekanisme katup merupakan sebuah mekanisme yang mengatur buka tutup katup IN dan EX sesuai dengan siklus kerjanya. Seperti yang kita tahu bersama bahwa pada cara kerja motor 4 tak, katup IN akan membuka ketika langkah hisap untuk memasukkan campuran udara dan bahan bakar ke silinder. Dan katup EX akan membuka ketika langkah buang untuk membuang gas sisa-sisa pembakaran. Mekanisme yang mengatur buka tutup kedua katup ini disebut dengan  mekanisme katup , secara garis besar  mekanisme katup  ini terbagi menjadi dua macam yaitu OHV  (Over Head Valve)  dan OHC  (Over Head Camshaft) . Untuk jenis OHC masih dibagi lagi menjadi dua versi yaitu SOHC  (Single Over Head Camshaft)  dan DOHC  (Double Over Head Camshaft) . Sekilas Perbedaan Mekanisme Katup tipe OHV dan DOHC Mekanisme Katup Mekanisme katup tipe OHV  (Over Head Valve)  memiliki ciri khusus yaitu letak ...
Post a Comment
Read more

Contoh Notice,Warning,Caution

Contoh  Notice, Warning, Caution Notice. Notice  merupakan salah satu jenis  short functional text  yang berisi sebuah informasi singkat dan sederhana yang berbentuk tulisan/gambar/tanda/ simbol untuk memberikan informasi, instruksi atau peringatan kepada publik dan biasanya berbentuk rambu-rambu. Berikut beberapa contoh  notice : (Perhatian: Jas laboratorium harus dipakai di daerah ini)    (Perhatian: Dilarang parkir disini) (Perhatian: Parkir mobil ini dibawah pengawasan CCTV) Notice di Sekolah Students Must Turn of Cellular Phones Before Entering School Building Contoh di atas bermakna : Siswa harus mematikan HP sebelum memasuki bangunan sekolah. Cell Phone Use Prohibited on School Grounds Contoh di atas bermakna : Penggunaan HP dilarang di wilayah sekolah. No Cell Phone Use in this Classroom Contoh di atas bermakna : Dilarang Menggunakan HP di Kelas Please No Texting Contoh di atas bermakna : Moho...
Post a Comment
Read more