Skip to main content

Pengertian Prisma dan Limas

Pengertian Prisma dan Limas

Pada pembahasan sebelumnya, kalian telah mempelajari bangun ruang kubus dan balok. Sedangkan pada pembahasan kali ini kita akan mempelajari bentuk bagun ruang yang lain, yaitu prisma dan limas. Apakah yang dimaksud dengan bangun ruang prisma dan limas?

1. Pengertian Prisma

Perhatikan gambar bangun ruang berikut!
Macam-macam Jenis Prisma
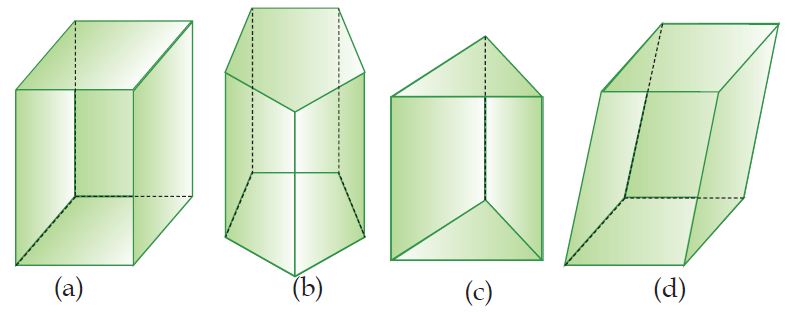
Gambar: Macam-macam Jenis Prisma
Bangun-bangun ruang di atas semuanya mempunyai dua bidang yang sejajar serta bidang-bidang lainnya berpotongan menurut garis-garis yang sejajar. Bangun-bangun ruang seperti inilah yang dinamakan prisma.
Jadi prisma adalah bangun ruang yang memiliki sepasang bidang sejajar dan kongruen yang merupakan alas dan tutup.
Sedangkan bidang-bidang lainnya diperoleh dengan menghubungkan titik-titik sudut dari dua bidang yang sejajar.

Macam-macam Jenis Prisma

Jenis prisma ada beberapa macam yang diberi nama sesuai bentuk alas prisma. Contoh, gambar (a) dinamakan prisma segi empat karena dua bidang yang sejajar berupa segi empat. Gambar (b) dinamakan prisma segilima, sedangkan gambar (c) dinamakan prisma segitiga.
Jika kita perhatikan semua prisma (a), (b), dan (c) mempunyai rusuk-rusuk yang tegak. Prisma seperti ini dinamakan prisma tegak.
Sebaliknya jika kita perhatikan gambar prisma (d) mempunyai rusuk-rusuk tidak tegak lurus dengan alas dan tutupnya. Prisma seperti ini dinamakan prisma miring. Pada pembahasan ini, kita akan membahas prisma tegak saja.

2. Pengertian Limas

Sekarang perhatikan bangun-bangun ruang di bawah ini!
Macam-macam Jenis Limas
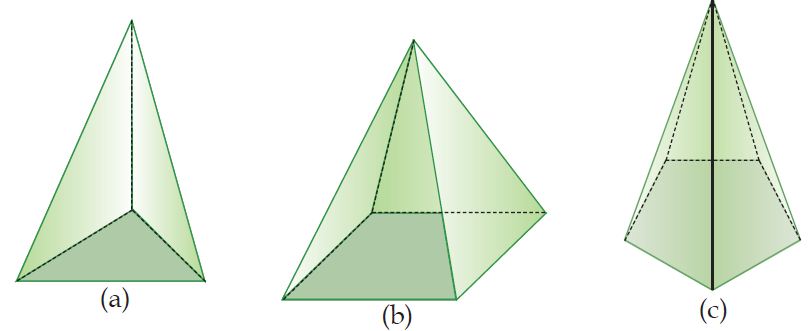
Gambar: Macam-macam Jenis Limas
Bangun-bangun ruang di atas memiliki satu bidang sebagai alas, sedangkan bidang-bidang lainnya berbentuk segitiga yang bertemu pada satu titik puncak. Bangun ruang seperti inilah yang dinamakan limas.
Limas adalah bangun yang dibatasi oleh sebuah segi-n sebagai alas dan n buah bidang berbentuk segi tiga yang bertemu pada suatu pucak.Limas dinamakan berdasarkan jenis alasnya, misalnya limas segitiga, limas segi enpat, limas segi lima, dll.

Macam-macam Jenis Limas

Jenis limas ada beberapa macam dan diberi nama sesuai dengan bentuk bidang alasnya. Misalnya, gambar (a) dinamakan limas segitiga, gambar (b) disebut limas segiempat, sedangkan gambar (c) dinamakan limas segilima. Dapatkah kamu menyebutkan bentuk limas yang lain?



Bagian bagian Prisma dan Limas

Cobalah ingat kembali definisi-definisi dari bidang, rusuk, titik sudut, diagonal bidang, dan diagonal ruang sebuah bangun ruang.

Unsur-unsur Prisma

Pelajarilah contoh yang membahas prisma berikut ini.
Gambar di bawah ini adalah prisma segilima ABCDE.FGHIJ. Bidang pada prisma tersebut adalah ABCDE (bidang alas) dan FGHIJ (bidang tutup) yang berbentuk segilima. Sedangkan bidang-bidang tegaknya, yaitu ABGF, BCHG, CDIH, DEJI, dan EAFJ yang berbentuk persegi panjang.
Prisma Segi Lima
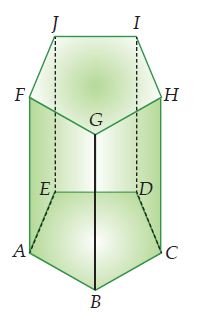Gambar: Prisma Segi Lima
Jumlah rusuk pada prisma segilima ini adalah 15 buah, dengan rusuk tegaknya adalah AF, BG, CH, DI, dan EJ. Sedangkan rusuk-rusuk lainnya adalah AB, BC, CD, DE, EA, FG, GH, HI, JF, dan IJ.

Unsur-unsur Limas

Selanjutnya, pelajarilah contoh limas berikut ini. Gambar di bawah ini adalah limas segiempat T.ABCD.
Limas Segi Empat
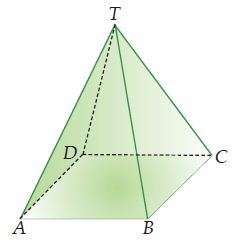Gambar: Limas Segi Empat
Bidang alas limas tersebut, yaitu ABCD, berbentuk segiempat, serta bidang-bidang tegak lainnya, yaitu TAB, TBC, TCD, dan TAD berbentuk segitiga.
Jumlah rusuk limas segiempat ini adalah 8 buah. Rusuk tegaknya adalah TA, TB, TC, dan TD, sedangkan rusuk-rusuk lainnya adalah AB, BC, CD, dan DA.

1. Bidang Diagonal Prisma

Perhatikan gambar berikut ini!
Bidang Diagonal Prisma
Gambar: Bidang Diagonal Prisma
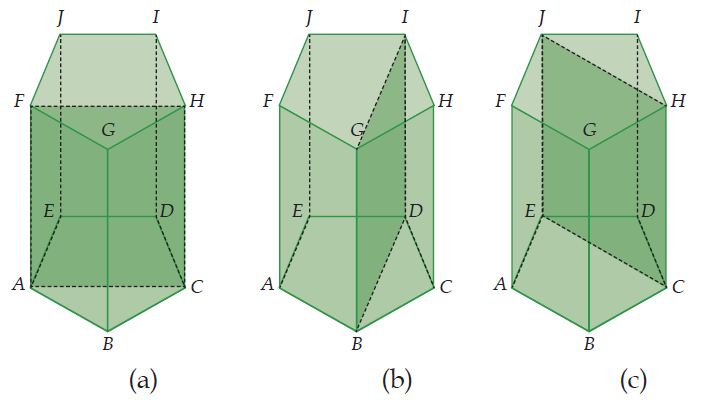
Gambar di atas merupakan gambar prisma segilima beraturan ABCDE.FGHIJ. Bidang ACHF pada gambar (a) merupa kan bidang diagonal prisma yang dibatasi oleh dua buah diagonal bidang, serta dua buah rusuk tegak.
Bidang seperti ACHF inilah yang dinamakan dengan bidang diagonal prisma. Dapatkah kamu menyebutkan bidang diagonal lainnya selain bidang ACHF pada prisma di atas? Coba kalian tunjukkan! Berapa banyak bidang diagonal lainnya yang dapat kamu temukan?
Perhatikan kembali bidang diagonal ACHF pada gambar (a). Bidang ini dibatasi oleh diagonal bidang AC dan FH yang saling sejajar dan sama panjang, serta dua rusuk tegak AF dan CH yang sejajar, sama panjang, dan tegak lurus dengan bidang alas dan tutup, maka bentuk dari bidang diagonal ACHF adalah persegi panjang. Selidikilah bentuk bidang diagonal yang lainnya!

2. Bidang Diagonal Limas

Perhatikan gambar di berikut!
Bidang Diagonal Limas
Gambar: Bidang Diagonal Limas
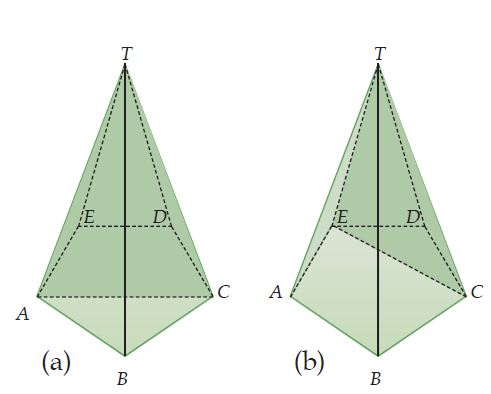
Gambar di atas merupakan gambar limas segilima beraturan T.ABCDE. Bidang TAC pada gambar (a) dan bidang TEC pada gambar (b) merupakan bidang diagonal limas T.ABCDE. Bidang diagonal limas dibatasi oleh satu buah diagonal bidang dan dua buah rusuk limas.
Dari gambar, terlihat bahwa bidang diagonal limas berbentuk segitiga dengan sisi alas merupakan diagonal bidang alas limas tersebut.

Luas Permukaan Prisma

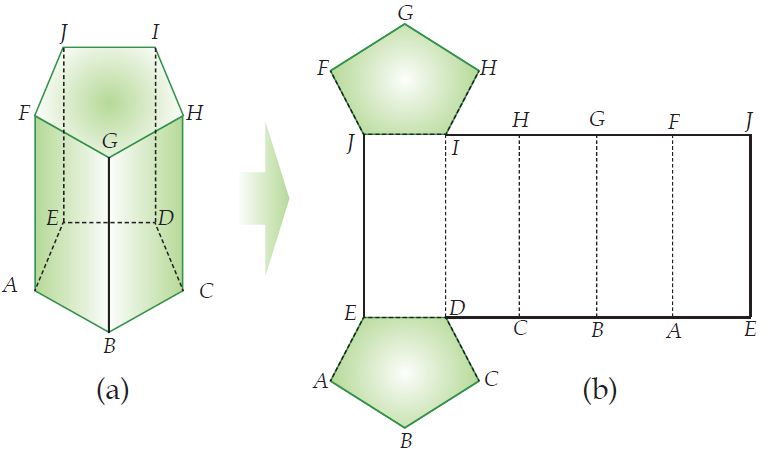
Misalkan kita memiliki prisma segilima ABCDE.FGHIJ seperti terlihat pada gambar (a) dan bentuk jaring-jaringnya pada gambar (b). Maka luas permukaan prisma adalah sebagai berikut.
Prisma Segi Lima
Gambar: Prisma Segi Lima
Luas permukaan prisma segilima ABCDE.FGHIJ = luas bidang EABCD + luas bidang IHGFJ + luas bidang EDIJ + luas bidang DCHI + luas bidang CBGH + luas bidang BAFG + luas bidang AEJF
Karena bidang alas dan bidang tutup prisma kongruen, maka luas EABCD = luas IHGFJ, sehingga dapat dinyatakan dalam bentuk berikut.
Luas permukaan prisma = luas bidang EABCD + luas bidang EABCD + a × t + a × t + a × t + a × t + a × t
= 2 × luas EABCD + (a + a + a + a + a) × t
= (2 × luas alas) + (keliling alas × tinggi prisma)

Rumus Luas Permukaan Prisma

Maka untuk setiap prisma berlaku rumus:
Rumus Luas Permukaan Prisma dan Contoh Soalnya

Contoh Soal Luas Permukaan Prisma

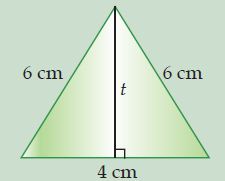
Alas sebuah prisma berbentuk segitiga sama kaki dengan panjang sisi-sisinya 6 cm, 6 cm dan 4 cm. Jika tinggi prisma 9 cm, hitunglah luas permukaan prisma tersebut!
Rumus Luas Permukaan Prisma dan Contoh Soalnya
Penyelesaian:
Terlebih dahulu kita harus mencari tinggi segitiga alasnya.
t = √62 – 22
  = √36 – 4
  = √32
  = 4√2 cm
  = 5,66 cm
Luas permukaan prisma
  = 2 × luas alas + (keliling alas × tinggi prisma)
  = (2 × ½ × 4 × 5,66) + [(6 + 6 + 4) × 9]
  = 22,63 + 144
  = 166,63 cm2.

Volume Prisma

Volume merupakan isi dari suatu bangun ruang. Volume bangun ruang dapat ditentukan dengan menggunakan rumus.
Untuk menentukan rumus umum volume sebuah prisma, marilah kita tinjau rumus volume prisma segitiga. Rumus volume prisma segitiga dapat diturunkan dari rumus volume balok. Perhatikanlah gambar berikut ini.
Prisma Segi Empat
Gambar: Prisma Segi Empat 
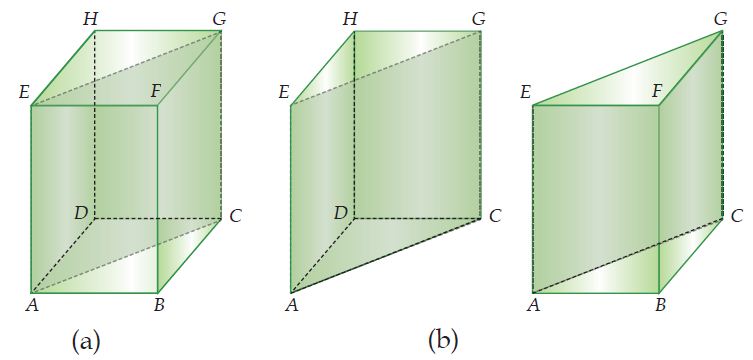
Jika balok ABCD.EFGH pada gambar (a) dibagi dua melalui bidang diagonal ACGE, maka akan diperoleh dua buah prisma segitiga, yaitu prisma ACD.EGH dan prisma ABC.EFG.
Karena bidang diagonal balok membagi balok menjadi dua bagian sama besar, maka volume balok sama dengan dua kali volume prisma segitiga. Maka volume prisma segitiga dapat dirumuskan:
Volume prisma segitiga = 12 × volume balok ABCD.EFGH
                                       = 12 × AB × BC × CG
                                       = 12 × luas bidang ABCD × CG
                                       = 12 × (luas ΔABC + luas ΔACD) × CG
                                       = 12 × (2 × luas ΔABC) × CG
                                       = luas ΔABC × CG
                                       = luas alas × tinggi prisma
Apakah untuk menentukan rumus volume prisma yang lain dapat menggunakan rumus volume prisma segitiga? Perhatikan gambar di bawah ini!
Prisma Segi Enam
Gambar: Prisma Segi Enam
Jika prisma segienam beraturan kita iris pada bidang diagonal ADJG, bidang diagonal BEKH, dan bidang diagonal CFLI, maka kita akan mendapatkan enam buah prisma segitiga beraturan. Maka volume prisma segienam dapat dinyatakan dalam bentuk berikut.
Volume prisma segienam ABDEF.GHIJKL
                     = 6 × volume prisma segitiga BCO.HIT
                     = 6 × luas BCO × TO
                     = luas segienam ABCDEF × TO
                     = luas alas × tinggi prisma

Rumus Volume Prisma

Maka untuk setiap prisma berlaku rumus:
Rumus Volume Prisma dan Contoh Soal Volume Prisma

Contoh Soal Volume Prisma

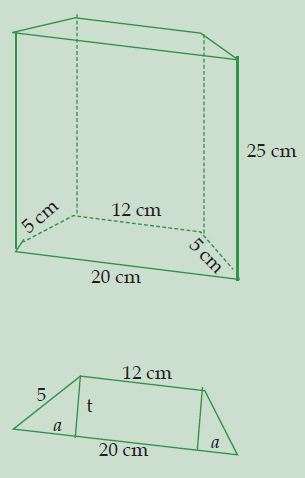
Alas sebuah prisma berbentuk trapesium sama kaki dengan panjang sisi-sisi sejajarnya adalah 12 cm dan 20 cm, serta sisi miringnya 5 cm. Jika tinggi prisma tersebut 25 cm, hitunglah volume prisma!
Rumus Volume Prisma dan Contoh Soal Volume Prisma
Penyelesaian:
Sebelum mencari volume prisma, kita harus mencari luas alas prisma tersebut.
2a = 20 – 12 = 8
a = 4 cm
t = √52 – 42
  = √25 – 16
  = √9
  = 3 cm
Luas alas = (20 + 12):2 × 3
= 32:2 × 3
= 16 × 3
= 48 cm2
Jadi, volume prisma adalah:
V = luas alas × tinggi prisma
   = 48 × 25  
   = 1.200 cm3.

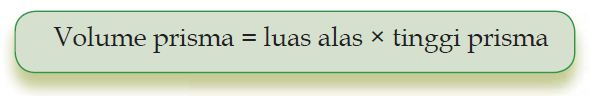
Comments

Post a Comment

Popular posts from this blog

MENGANALISIS KARYA SENI RUPA 2 DIMENSI

MENGANALISIS KARYA SENI RUPA 2 DIMENSI BARONG & LEAK ·       Karya : Afandi (1980) ·       Fungsi  : sebagai hiasan dalam ruangan dan merupakan  bagian seni kebudayaan dari Masyarakat Bali, dimana Barong dan Leak adalah filosofi bagaimana bertolak belakangnya antara kebaikan dan kejahatan. Lukisan ini juga sebagai saluran imajinasi pelukis. ·       Media Alat dan Bahan  :  Oil on Canvas .  Cat Minyak diatas canvas adalah bahan yang paling populer, dan biasa digunakan dalam melukis, karena pemakaian yang mudah diaplikasikan serta hasil lukisanya bisa digunakan dalam berbagai tehnik gaya lukisan, halus ataupun bertekstur. Bahan melukis ini berbasis minyak, dan memiliki tingkatan kualitas mulai dari kualitas normal hingga kualitas tinggi, dan dibedakan dengan harga. Baik pelukis pemula atau pelukis handal, sering menggunakan bahan material cat minyak dan canvas sebag...
Post a Comment
Read more

pengertian sistem suspensi pada kendaraan

sistem suspensi pada kendaraan  berfungsi untuk menghubungkan bodi kendaraan dengan roda, kontruksinya dibuat sedemikian rupa agar dapat menyerap getaran, oskilasi dan kejutan sebagai akibat dari kondisi dan permukaan jalan yang tidak rata, sehingga diperoleh keamanan dan kenyamanan ketika berkendara. Sistem suspensi  juga berfungsi untuk memindahkan gaya pengereman dan gaya gerak ke body melalui gesekan antara jalan dengan roda-roda. Fungsi terakhir dari sistem suspensi adalah untuk menopang body pada axle dan memelihara letak geometris antara body dan roda-roda. Dengan adanya sistem suspensi, maka kendaraan akan lebih stabil baik ketika terjadi pengereman, belokan, sampai jalan yang bergelombang atau tidak rata. Suspensi juga akan membuat pengendara merasakan kenikmatan dan stabilitas ketika mengendarai.  Syarat-syarat Sistem Suspensi Dalam menjalankan fungsinya, suspensi harus dapat memiliki beberapa syarat yaitu : Mengantar gerakan roda. Memungkinkan...
Post a Comment
Read more

Menganalisis Karya Seni Rupa Murni

"Menganalisis Karya Seni Rupa Murni",    1. Pertama, yaitu Borobudur Pagi Hari Judul : Borobudur Pagi Hari Tahun : 1983 Ukuran : 150 cm x 200 cm Media : Cat Minyak “Borobudur Pagi Hari” merupakan salah satu karya Affandi yang terinspirasi oleh megahnya candi Borobudur dan lingkungan sekitar pada masa itu, saat Affandi melintas dan memperhatikan Borobudur di pagi hari. Obyek matahari selalu menarik perhatian di beberapa karya beliau sebagai fokus pendukung utama. Warna – warna dingin dan suasana tenang mendominasi lukisan ini karena melukiskan suasana pagi hari yang cerah . Dan dilukisan ini Affandy lebih nenonjolkan obyek alam sebagai latar belakang. Perpaduan warna yang digunakan semakin menghidupkan lukisan tersebut karena warna yang digunakan padu antara warna satu dengan warna yang lain. Dan dilukisan tersebut gambar candi Borobudur terlihat sangat jelas tanpa kita harus menganalisis makna lukisan tersebut. Dan bentuk mataharinya tidak menyerupai matahari tet...
Post a Comment
Read more