Pengertian Prisma

Pengertian prisma

Prisma adalah bangun ruang yang memiliki alas dan atap yang sama bentuk dan ukurannya serta memiliki sisi bagian samping yang berbentuk persegi panjang.

Menurut kamus besar bahasa Indonesia, prisma berarti zat padat yang mempunyai bentuk geometris dengan dua bidang sejajar yang identik.

Jenis-jenis prisma

Berdasarkan pengertian di atas, maka prisma mempunyai bentuk yang sangat beragam diantranya adalah;

1. Prisma segitiga

Prisma segitiga adalah prisma yang mempunyai alas segi tiga, apapun jenis segitiganya; bisa segitiga sama kaki, segitiga sama sisi, sigitiga siku-siku maupun segitiga sembarang.

Menurut kamus besar bahasa Indonesia, prisma segitiga adalah bentuk tertutup oleh gabungan dua daerah berbentuk segitiga dan tiga daerah berbentuk empat persegi panjang.

Sifat-sifat prisma segitiga

Untuk lebih memudahkan dalam memahami tentang sifat-sifat pada prisma sigitiga, silahkan perhatikan gambar prisma segitiga berikut ini!

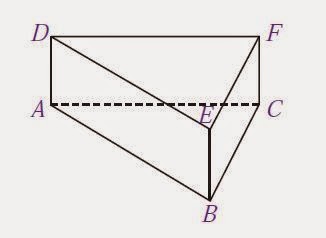Gambar: Prisma Segitiga ABC.DEF

Berdasarkan gambar tersebut di atas, dapat disimpulkan bahwa prisma tersebut memiliki sifat-sifat sebagai berikut:

a. Prisma memiliki bentuk alas dan atap yang kongruen.

Pada gambar terlihat bahwa segitiga ABC dan DEF memiliki ukuran dan bentuk yang sama.

b. Setiap sisi bagian samping prisma berbentuk persegi panjang. 

Prisma segitiga pada gambar dibatasi oleh tiga persegi panjang di setiap sisi sampingnya, yaitu ABED, BCFE, dan ACFD.

c. Prisma memiliki rusuk tegak.

Perhatikan prisma segitiga pada gambar. Prisma tersebut memiliki tiga buah rusuk tegak, yaitu AD, BE, dan CF. Rusuk tersebut dikatakan tegak karena letaknya tegak lurus terhadap bidang alas dan atas.

Dalam kondisi lain, ada juga prisma yang rusuknya tidak tegak, prisma tersebut disebut prisma sisi miring.

d. Setiap diagonal bidang pada sisi yang sama memiliki ukuran yang sama.

Prisma segitiga ABC.DEF pada gambar diagonal bidang pada sisi ABED memiliki ukuran yang sama panjang. Perhatikan bahwa AE = BD, BF = CE, dan AF = CD.

Jaring-jaring prisma segitiga

Untuk mendapatkan jaring-jaring pada prisma segitiga yaitu dengan cara membuka sisi-sisinya, sebagaiman terlihat pada gambar berikut ini.

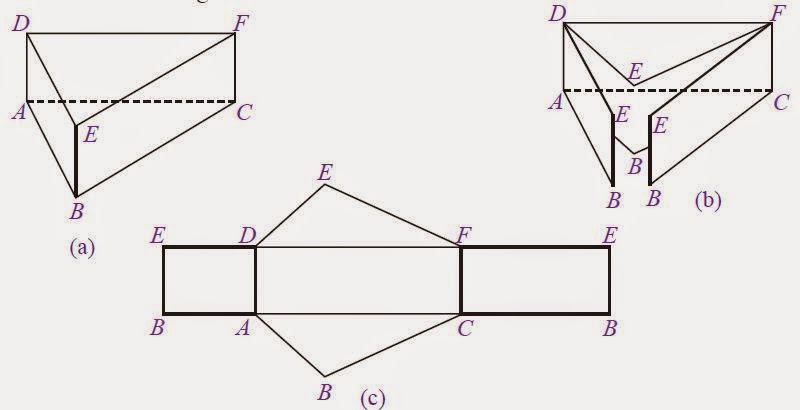
Untuk contoh lain dari jaring-jaring prisma segitiga dapat dilihat pada gambar berikut ini!

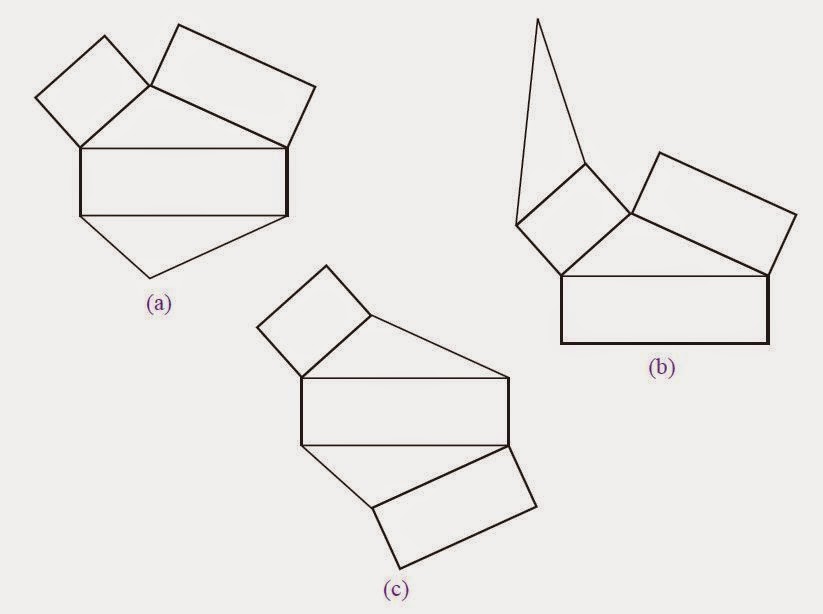Contoh Jaring-jaring Prisma segi tiga

2. Prisma segi empat

Istilah lain dari prisma segi empat adalah kubus atau blok, sehingga tidak masuk dalam pembahasan prisma.

3. Prisma segi lima

Prisma segi lima adalah prisma yang memiliki alas dan atap berbentuk segi lima.

Jaring-jaring prisma segi lima

Sama halnya dengan prisma segitiga, untuk mendapatkan jaring-jaring pada prisma segi lima juga dapat dilakukan dengan cara membuka sisi-sisi pada prisma tersebut, sebagaimana gambar berikut ini!

Berikut ini adalah contoh lain dari jaring-jaring segi lima:

4. Prisma segi enam

Prisma segi enam adalah prisma yang memiliki alas dan atap berbentuk segi enam.

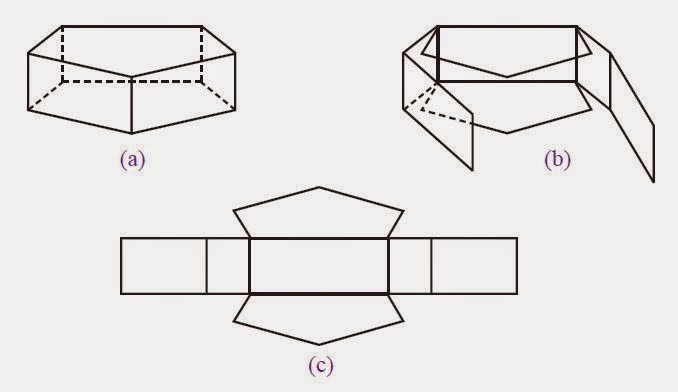
Jaring-jaring prisma segi enam

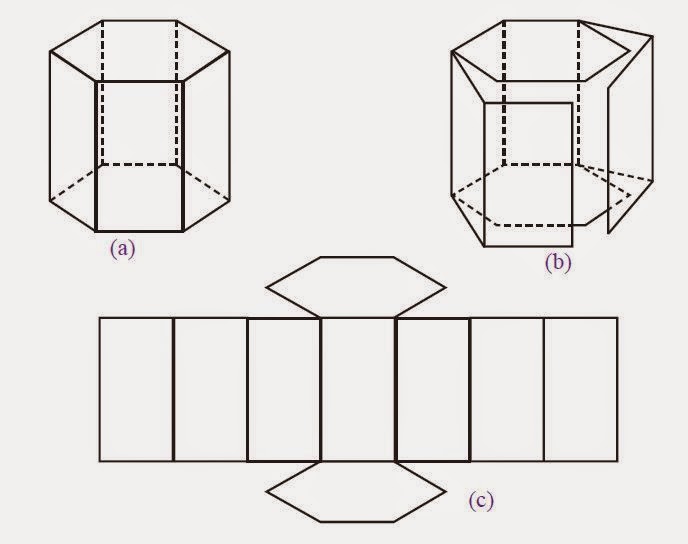
Untuk mendapatkan jaring-jaring pada prisma segi enam juga sama dengan cara-cara yang lainnya, yaitu dengan cara membuka sisi-sisi pada prisma tersebut. Perhatikan gambar berikut ini.

Unsur-unsur prisma segi enam

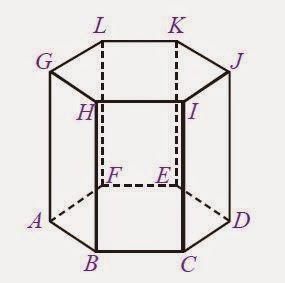
Untuk lebih memudahkan dalam memahami unsur-unsur prisma segi enam, silahkan perhatikan gambar berikut ini!

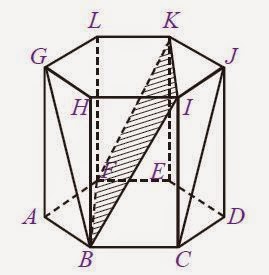Gambar: Prisma segi enam ABCDEF.GHIJKL

Diantara unsur-unsur prisma adalah sebagai berikut;

1. Sisi atau Bidang

Terdapat 8 sisi atau bidang yang dimiliki oleh prisma segienam, yaitu;
1. Sisi ABCDEF (sisi alas),
2. Sisi GHIJKL (sisi atas),
3. Sisi BCIH (sisi depan),
4. Sisi FEKL (sisi belakang),
5. Sisi ABHG (sisi depan kanan),
6. Sisi AFLG (sisi belakang kanan),
7. Sisi CDJI (sisi depan kiri), dan
8. Sisi DEKJ (sisi belakang kiri).

2. Rusuk

Dari Gambar tersebut di atas , terlihat bahwa prisma segienam ABCDEF.GHIJKL memiliki 18 rusuk, 6 di antaranya adalah rusuk tegak. Rusuk-rusuk tersebut adalah AB, BC, CD, DE, EF, FA, GH, HI, IJ, JK, KL, LG, dan rusuk-rusuk tegaknya adalah AG, BH, CI, DJ, EK, FL.

3. Titik Sudut

Prisma segienam ABCDEF.GHIJKL memiliki 12 titik sudut. Dari Gambar tersebut di atas, terlihat bahwa titik-titik sudut tersebut adalah A, B, C, D, E, F, G, H, I, J, K, dan L. Selain unsur-unsur yang telah disebutkan, prisma pun memiliki istilah diagonal bidang dan bidang diagonal. Untuk lebih jelasnya, coba kamu perhatikan dan pelajari uraian berikut.

4. Diagonal Bidang

Coba kamu perhatikan prisma segienam ABCDEF. GHIJKL pada Gambar tersebut. Dari gambar tersebut terlihat ruas garis BG yang terletak di sisi depan kanan (sisi tegak) ditarik dari dua titik sudut yang saling berhadapan sehingga ruas garis BG disebut sebagai diagonal bidang pada bidang prisma segienam ABCDEF. GHIJKL.

Begitu pula dengan ruas garis CJ pada bidang CDIJ. Ruas garis tersebut merupakan diagonal bidang pada prisma segienam ABCDEF. GHIJKL. Pada prisma segi enam ABCDEF. GHIJKL memiliki 16 diagonal bidang atau diagonal sisi.

5. Bidang Diagonal

Sekarang, coba kamu perhatikan prisma segienam ABCDEF.GHIJKL pada Gambar tersebut diatas. Pada prisma segienam tersebut, terdapat dua buah diagonal bidang yang sejajar yaitu BI dan FK.

Kedua diagonal bidang tersebut beserta ruas garis KI dan FB membentuk suatu bidang di dalam prisma segienam ABCDEF.GHIJKL. Bidang tersebut adalah bidang BFKI yang merupakan bidang diagonal prisma segienam. Coba kamu sebutkan bidang diagonal yang lain dari prisma segienam pada Gambar tersebut di atas!

6. Diagonal Ruang

Selain diagonal bidang dan bidang diagonal, pada prisma segi enam juga terdapat diagonal ruang. Untuk prisma segi enam ABCDEF.GHIJKL memiliki 36 diagonal ruang AI, AJ, AK, BJ, BK, BL dan seterusnya.

5. Dan seterusnya

Sebenarnya tidak ada batasan untuk bentuk prisma, namun dalam pembahasan kali ini kita hanya membatasi pembahasan pada prisma segi enam, prisma segi lima dan prisma segi tiga.

Untuk lebih jelas dan memudahkan untuk memahami tentang pengertian prisma dan berbagai macam jenisnya, silahkan perhatikan gambar di bawah ini!

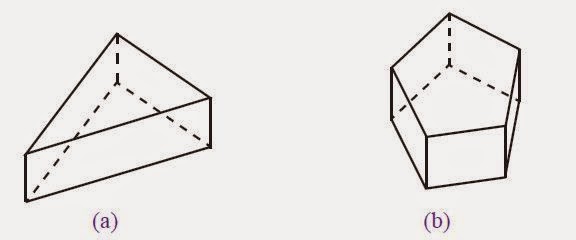Macam-macam Prisma

(c)

Keterangan Gambar:
Gambar (a) merupakan contoh bentuk prisma segitiga dan gambar (b) merupakan contoh bentuk prisma segi lima, selanjutnya gambar (c) merupakan contoh bentuk prisma segi enam.

Rumus luas permukaan prisma

Sama seperti kubus dan balok, asal usul menentukan luas permukaan prisma dapat dihitung menggunakan jaring-jaring prisma tersebut. Caranya adalah dengan menjumlahkan semua luas bangun datar pada jaring-jaring prisma.

Untuk lebih jelasnya silahkan perhatikan prisma segitiga berikut ini beserta jaring-jaringnya!

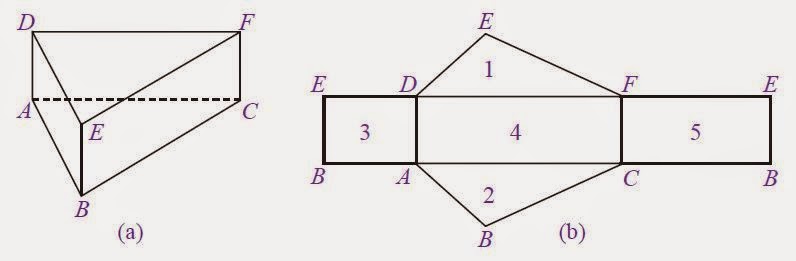Gambar: Asal Usul Rumus Luas permukaan prisma

Dari gambar tersebut di atas, terlihat bahwa prisma segitiga ABC.DEF memiliki sepasang segitiga yang identik dan tiga buah persegipanjang sebagai sisi tegak. Dengan demikian, luas permukaan prisma segitiga tersebut adalah;

Luas permukaan prisma = luas ΔABC + luas ΔDEF + luas EDAB + luas DFCA + luas FEBC
                                      = 2 x luas ΔABC + luas EDBA + luas DFAC + luas FEBC
                                      = (2 x luas alas) + (luas bidang-bidang tegak)

Jadi, luas permukaan dapat dinyatakan dengan rumus sebagai berikut.

Luas permukaan prisma = 2 x luas alas + luas bidang-bidang tegak

Rumus volume prisma

Untuk lebih memahami asal-usul rumus volume prisma, silahkan perhatikan gambar berikut ini!

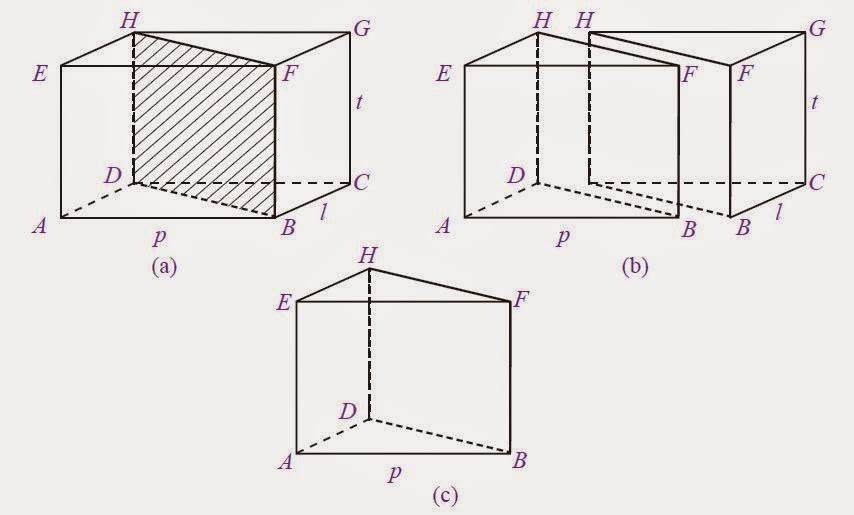Gambar: Asal usul rumus volume prisma

Pada gambar tersebut di atas, memperlihatkan sebuah balok ABCD.EFGH yang dibagi dua secara melintang. Ternyata, hasil belahan balok tersebut membentuk prisma segitiga, seperti pada Gambar (b). Perhatikan prisma segitiga BCD.FGH pada Gambar (c) . Dengan demikian, volume prisma segitiga adalah setengah kali volume balok.

Volume prisma BCD.FGH = ½ × volume balok ABCD.EFGH
                                           = ½ × (p × l × t)
                                           = ( ½ × p × l) × t
                                           = luas alas × tinggi

Jadi, volume prisma dapat dinyatakan dengan rumus sebagai berikut.

Volume prisma = luas alas × tinggi

Contoh soal dan pembahasannya

Perhatikan contoh soal berikut ini!

1. Perhatikan prisma segitiga pada gambar di bawah ini! Dari gambar tersebut, tentukan:
         a.  luas alas prisma segitiga!
         b. volume prisma segitiga!
2. Sebuah prisma memiliki volume 238 cm3 dan luas alas 34 cm2. Tentukan tinggi prisma tersebut!

Jawaban:

Silahkan Baca juga: